Given equations y =sin(x) y =e x= 0 x= 7 2 y = sin ( x) y = e x = 0 x = 7 2 Plotting the given equations on a graph Based on the graph, the area of the shaded region will be, A= ∫ 7 2 0Find stepbystep Calculus solutions and your answer to the following textbook question Solve the equation e^y y' cos x = 0 and graph several members of the family of solutions How does the solution curve change as the constant C varies?Solve y = e^0*sin 0, y = 1*0 = 0 From the graph of the curve given below, it can be seen that a tangent drawn at x = 0 passes through the origin The yintercept of the tangent to the curve y = e
Y E X Sin X Geogebra
Y=e^-x sinx graph
Y=e^-x sinx graph- 3D and Contour Grapher A graph in 3 dimensions is written in general z = f(x, y) That is, the z value is found by substituting in both an x value and a y value The first example we see below is the graph of z = sin (x) sin (y) It's a function of x and y You can use the following applet to explore 3D graphs and even create your own, using variables x and yPiece of cake Unlock StepbyStep Natural Language Math Input NEW Use textbook math notation to enter your math



Plot Help
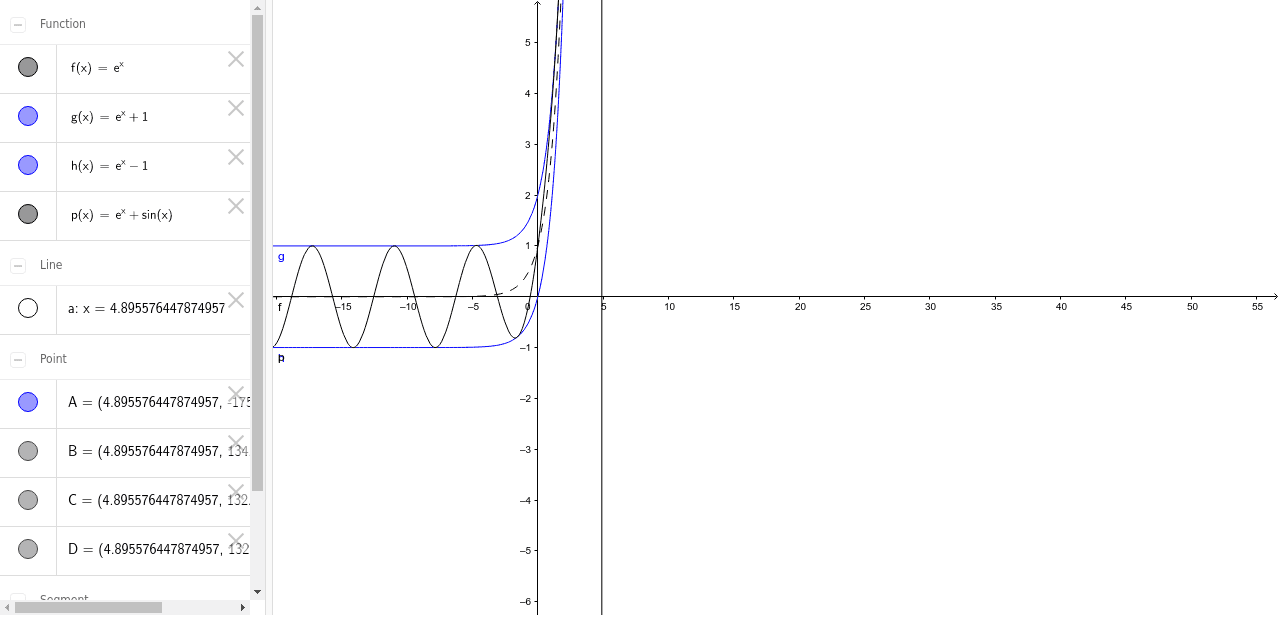
What we have right over here is the graph of y is equal to e to the X and what we're going to know by the end of this video is one of the most fascinating ideas in calculus and once again it reinforces the idea that E is really this somewhat magical number so we're going to do a little bit of an exploration let's just pick some points on this curve of y is equal to e to the X and think aboutGeneral Solution for y"y'=e^x sinx Thread starter shivers;This an interesting graph as e^x dominates the height of the y component and sin(x) provides a sharp periodicity in the right hand plane always crossing 0 at n*pi (n=1, 2, 3) When x is greater than about 10 for all practical purposes the graph is composed of vertical lines
Cosine Spaghetti Graphing Sine & Cosine Functions (Amp, Period, Vertical Shift Changes Only) PR2b1INET2 Sine and Cosine Graphing Template Solving 2Step Equations In Your HeadY = e(sin2x) dy/dx = d(e(sin2x))/dxxd(sin2x)/dx dy/dx = e(sin2x)xd(sin2x)/dx dy/dx = e(sin2x)x2xcos2x Hence Answer is;$$ 3x\sin x = e^x $$ I tried graphing it and could only find approximate solutions, not the exact solutions My friends said to use NewtonRaphson, Lagrange interpolation, etc, but I don't know what these are as they are much beyond the high school syllabus
How can we plot the following three functions f(x) = sin(x) k(x) = cos(x) u(x) = x² for x ∈ 0,1 on a single plot with the help of TikZ?Graph of sin (x) We will look at what the graph of the function y=sin (x) looks like by plotting values of sin (x) against the angle using the unit circle to help What is the maximum value of Sin (x)?The trigonometric functions cosine, sine, and tangent satisfy several properties of symmetry that are useful for understanding and evaluating these functions Now that we have the above identities, we can prove several other identities, as shown in the following example Using the properties of symmetry above, we can show that sine and cosine are special types of functions



4 2 Linear Approximations And Differentials Mathematics Libretexts



Ch 5 Array Computing And Curve Plotting
Dy/dx = 2cos2xe(sin2x) Draw the graph of y=e^x \sin x (without using a graph calculator) Draw the graph of y = exsinx (without using a graph calculator) https//mathstackexchangecom/questions//drawthegraphofyexsinxwithoutusingagraph Function problem (e^sin (x)) a) find the x and y coordinates of all maximum and minimum points on the given interval Justify your answers This is an AP exam question that is worth nine points (i cut out question b b/c it asks for sketching graph) Currently i have took the derivative of e^sin (x) and found cos (x)*e^sin (x) Setting theGraph y=e^ (x) y = e−x y = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0



All About E




Let R Be The Region Between The Graphs Of Y 1 And Y Sinx From X 0 To X Pi 2 How Do You Find The Volume Of Region R Revolved About The X Axis Socratic
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorIn this tutorial, we will learn how to plot a sine wave in Python w/ Matplotlib We will be plotting $\text{sin}(x)$ along with its multiple and submultiple angles Graph the parent function of color (blue) (y=f (x)=sin (x) Next graph the given function color (blue) (y=f (x)=sin 3x) The domain of this function is the set of input values for which the function f (x) is real and defined Hence, the domain of color (red) (f (x) is color (red) ( (oo, oo) The range of the function f (x) refers to the set of




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts



Control Tutorials For Matlab And Simulink Extras Plotting In Matlab
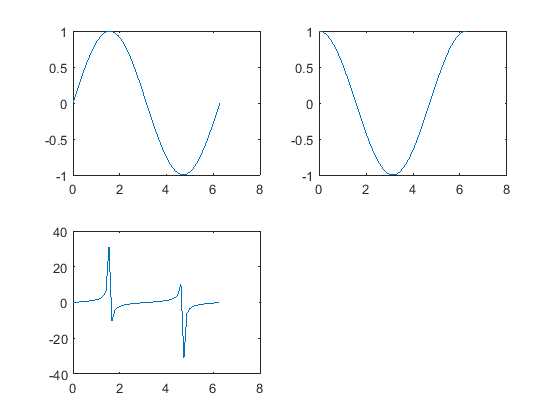
The easiest solution is to use the gradient function rather than diffThe gradient function produces a more accurate estimate and the output is the same length as the input, while the output of diff is one element shorter, owing to the different ways the two are calculatedFor graphs of the form $y=f(x)sinx$, draw the graphs of $y=f(x)$ and $y=f(x)$ Then draw the graph of $y=sinx$ with the usual roots but with the amplitude increasing or decreasing according to the values of $f$ The graphs should touch whenever $sinx$ reaches its maximum and minimum y e x D) y cosx E) y lnx APDifferentiation of y=e^(sinx) wrt to x My method ln both sides and then differientiate is that okay?



Consider The Function Defined By F X Sinx X If 1 X 0 Ax B If 0 X 1 And 1 Cosx X If X 1 How Do You Determine A And B Such




Pi Pops Up Where You Don T Expect It
Question Consider the function below z = sin (x) sin (y) OO > OO O (O (O (COCO (O OOO IV VI o (a) Match the function with its graph (labeled AF) A B D O E OF (b) Match the function with its contour map (labeled IVI) Ο Ι Ο ΙΙ III C IV V OVI Give reasons for your choices This function is periodic Ev in both x and y, but it is notSolve the differential equation {eq}y'' 2y' = e^x \sin x {/eq} by using the method of variation of parameters A straight line will be formed when graphing two variables, both in the firstSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



What Is Int Sinx Cosx Sqrt 1 Sin2x Dx Socratic



Solved Y 1 Sinx 2 0 Let R Be The Shaded Region In The Chegg Com
Ie ln y = sinx ln e = sinx 1/y (dy/dx) = co Step 1 (a) The function Find the y intercept Let the function Find the y intercept, by substituting in The y intercept is zero Step 2 (b) The function and the interval is Differentiate the function with respect to x Determination of critical pointsExample 1 Sketch the graph of y = 2 cos (x) 1 over one period Vertical Shift (translation) = 1 , up 1 unit We start by skeching y = cos (x) using the values of x and y from the unit circle (blue graph below) We then sketch y = 2 cos (x) streching y = cos (x) by 2 (green graph below) and finally y = 2 cos (x) 1 by shifting up 1 unit (red



Shift A Sine Function In A Graph Dummies



How Do You Show That The Function H X Xe Sinx Is Continuous On Its Domain And What Is The Domain Socratic
Move slider below to add more terms 3Graph sin x WolframAlpha Volume of a cylinder? sin (x π/2 ) = cos x y = cos x graph is the graph we get after shifting y = sin x to π/2 units to the left Period of the cosine function is 2π Max value of Graph Min value of the graph 1 at 0, 4π 1 at 2π There are a few similarities between the sine and cosine graphs, They are Both have the same curve which is shifted along the



1 Graphs Of Y A Sin X And Y A Cos X



Given F X E X Sinx On Pi Pi Identify The X And Y Intercepts Local Extrema And Inflection Points Use This Information To Sketch The Graph Can You Help Finding The Local Extrema Socratic
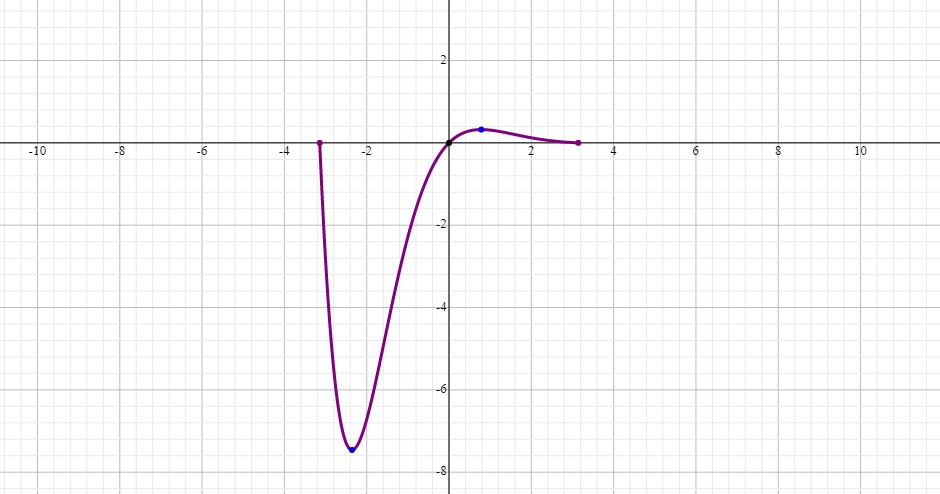
Plot sin x cos y WolframAlpha Area of a circle?Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build We now plug each of them into the function to find their ycoordinates x=(3pi)/4, y=e^(((3pi)/4))sin((3pi)/4)=e^((3pi)/4)sin((3pi)/4)=1055(sqrt2/2)=746 x=pi/4, y=e^(pi/4)sin(pi/4)=046(sqrt2/2)=033 Local Minimum (236, 746) Local Maximum (079, 033) To find the inflection point(s), we need to take the second derivative of the function and set it equal to 0 (d^2y)/dx^2=e^(x)sinx(e^(x)cosx)(e^(x)cosx(e^(x)sinx) (d^2y)/dx^2=e^(x)sinxe^(x)cosxe^(x)cosxe



Amy S Write Up 12
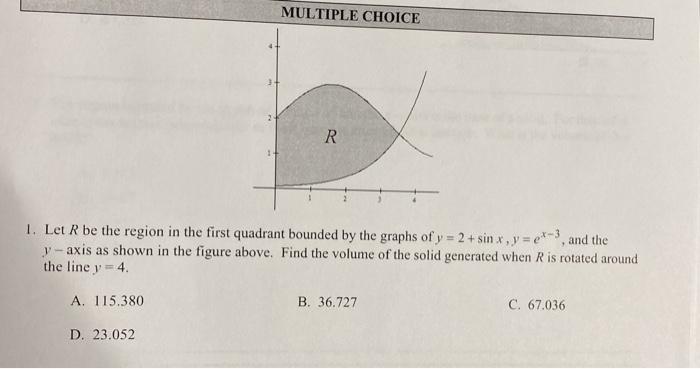



Solved Multiple Choice R 1 Let R Be The Region In The First Chegg Com
What is the minumum value of sin (x)?About Beyond simple math and grouping (like "(x2)(x4)"), there are some functions you can use as well Look below to see them all They are mostly standard functions written as you might expectFree derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graph



Examples Of Curve Sketching Calculus Socratic
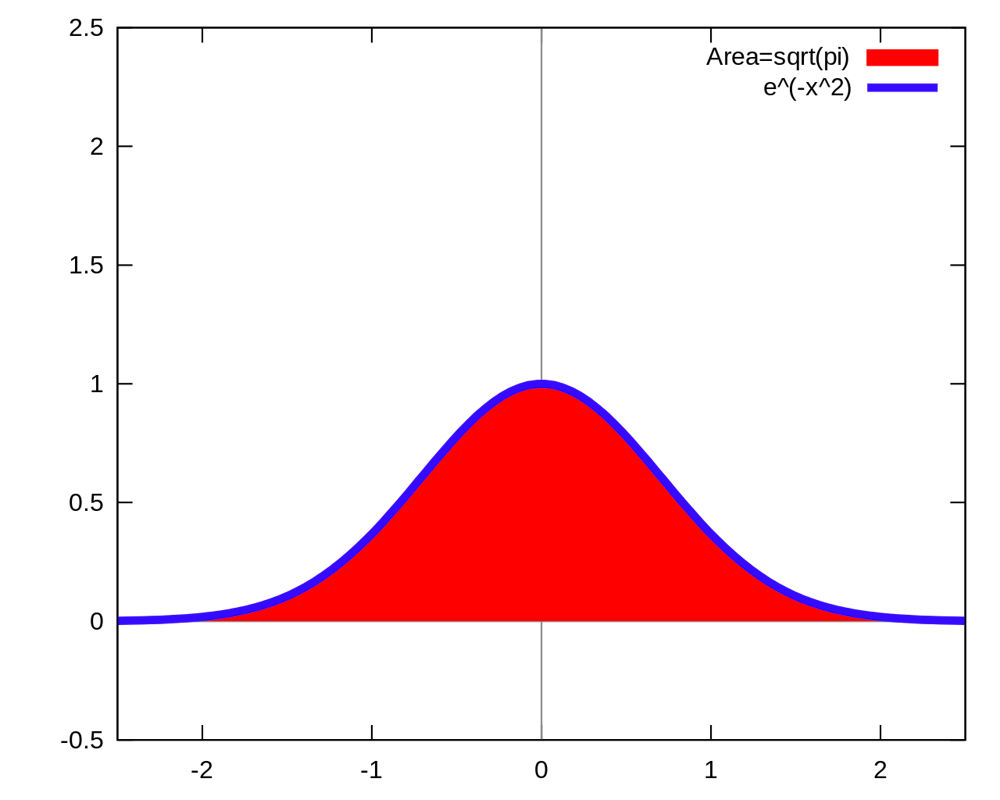



Pi Pops Up Where You Don T Expect It
Y = sinx y = sin(x 1) y = sin(x 2) Changing c effectively shifts the graph to the left or to the right This phase shift is determined by c/b For example, when c = 1 (graphed in red), the graph has the same period and amplitude as when c = 0 (graphed in pink), but has been shifted (1/1) = 1, or 1 unit to the leftGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!What do you think would happen if we continued the graph beyond an angle of 2pi radians?




Trigonometric Graph How To Draw Y Sin X Youtube



How To Draw The Graph Of Y Sin X Quora
Let a line through the origin intersect the unit circle, making an angle of θ with the positive half of the xaxisThe x and ycoordinates of this point of intersection are equal to cos(θ) and sin(θ), respectivelyThis definition is consistent with the rightangled triangle definition of sine and cosine when 0° < θ < 90° because the length of the hypotenuse of the unit circle is alwaysFunction will be reflected about the xaxis The graph of y = A sin x can be drawn by multiplying each value of the original function y = sin x by A The absolute value of the constant A is called the amplitude of the function Some graphical examples of the function y = A sin x for different values of A are shown belowY x ex 2 2 e−x − As x gets larger, ex increases quickly, but e−x decreases quickly So the second part of the difference ex/2 − e−x/2 gets very small as x gets large Therefore, as x gets larger, sinhx gets closer and closer to ex/2 We write this as sinhx ≈ ex 2 for large x But the graph of sinhx will always stay below the graph



What Is The Y Intercept Of The Tangent To The Curve Y E X Sin X At The Point Where X 0 Enotes Com



Plot Help
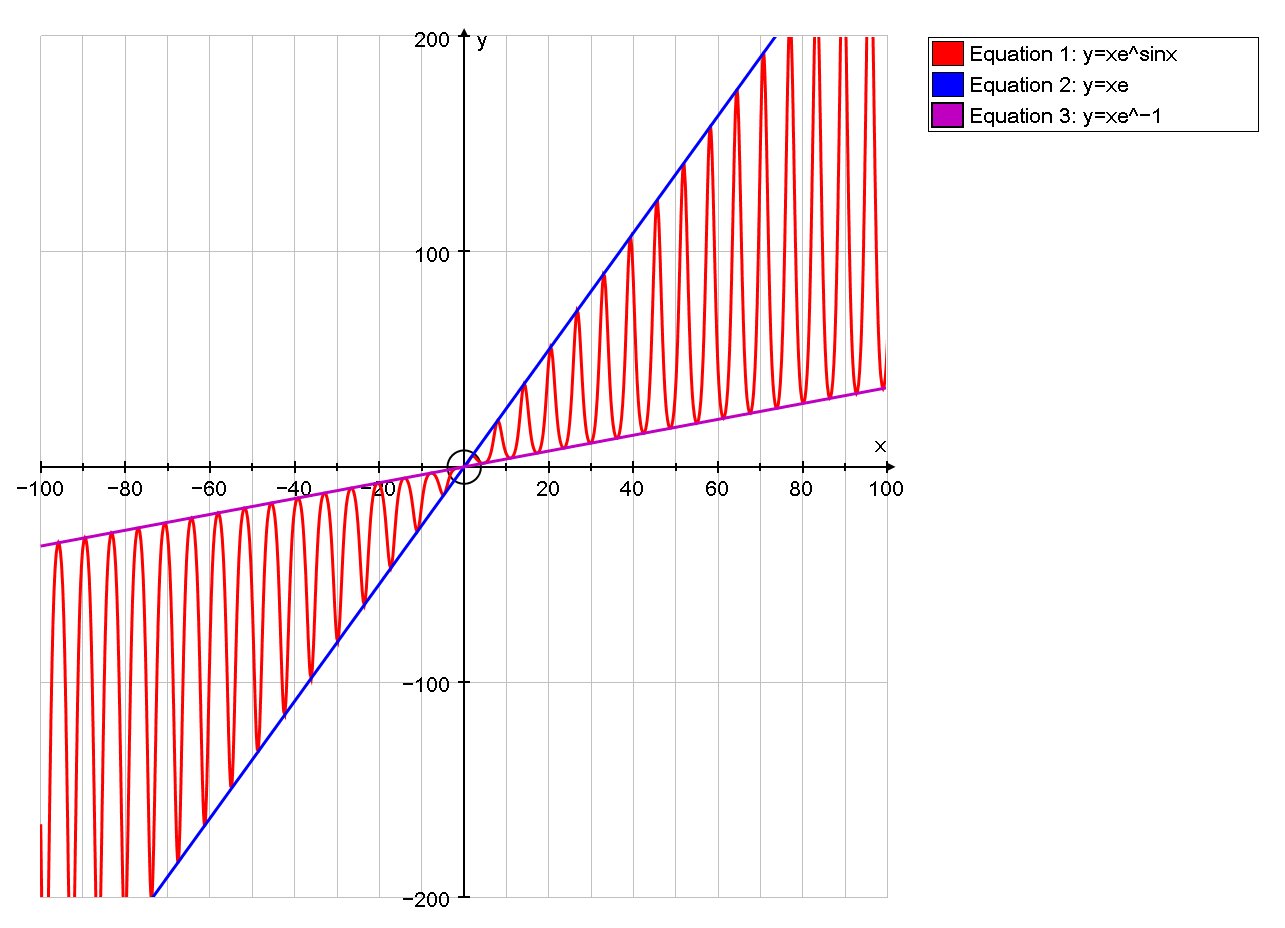
Now consider y = x sinx, when x is 0 it's the same as sinx when x is 1 it's higher and so on Here, x is continuous, so the value is constantly changing So you end up getting a sinx graph over y = x line Something like th Continue Reading y = sinx can be written as y = 0 sinx Some miscellaneous Graphs in mathematics y= xsinx, y= xsinx, y=e^xsinx, y=x^21/x Transformation Lecture 12Solution For Draw the graph of y=xsinx Solution For Draw the graph of y=xsinx Solution For Draw the graph of y=xsinx Become a Tutor Blog Cbse Question Bank Pdfs Mock Test Series New Download App Class 12 Math Calculus Curve Tracing 518 150 Draw




Transformation Of Graphs By Modulus Function Functions Openstax Cnx



Tamdistrict Org
The graph of y=sin (x) is like a wave that forever oscillates between 1 and 1, in a shape that repeats itself every 2π units Specifically, this means that the domain of sin (x) is all real numbers, and the range is 1,1 See how we find the graph of y=sin (x) using the unitcircle definition of sin (x) I understand that you're looking for the set of pairs $$ \{ (x,y) \in \mathbb R^2 y = \sin x \}$$ Since this is not in the form $"y=f(x)"$, its not a graph, but a more general collection of points In this specific case, you end up with filled in regions of the graph paper sinx would be a variable with a 4 character name, and would have nothing to do with the sine function, just like sinister would have nothing to do with the sine function The sine function applied to x would be sin(x)
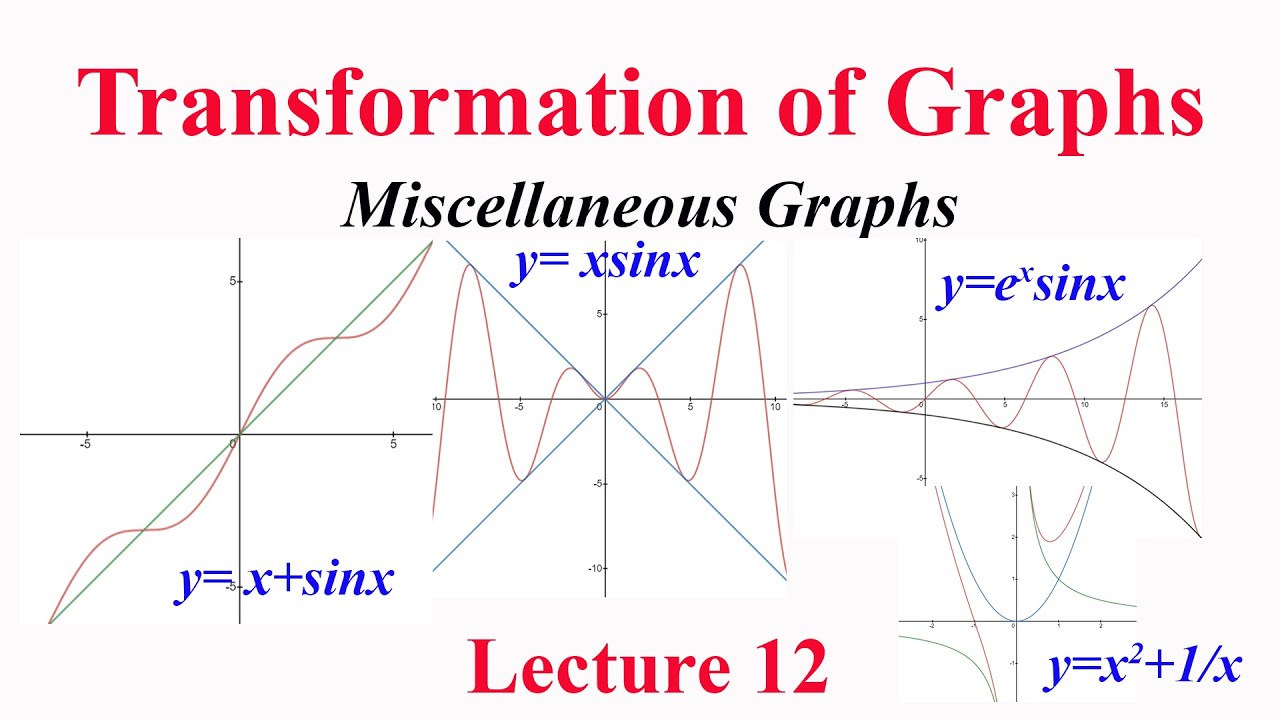



Miscellaneous Graphs Y X Sinx Y Xsinx Y E Xsinx Y X 2 1 X Transformation Lecture 12 Youtube
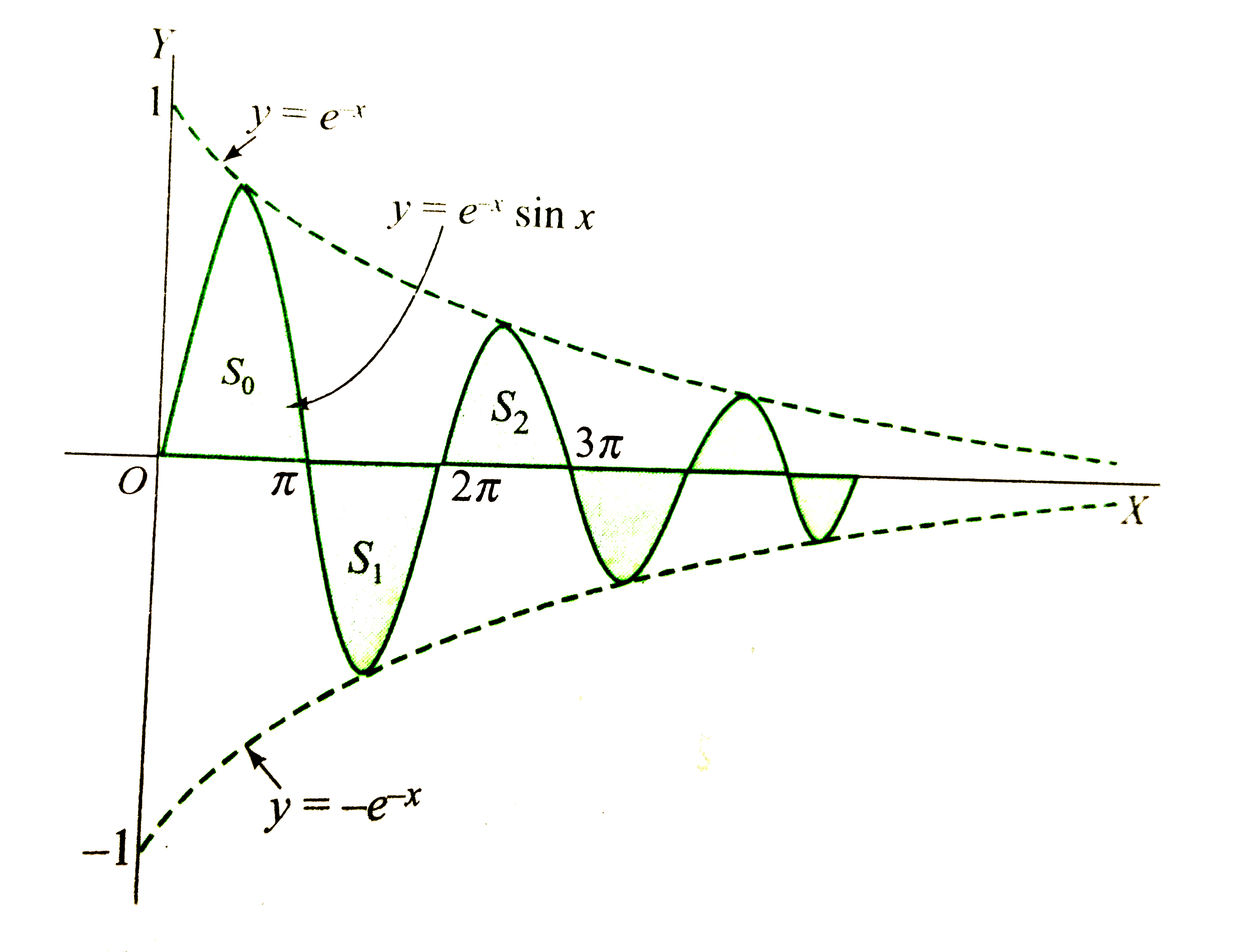



Consider The Sequence Of Natural Numbers S 0 S 1 S 2 Such
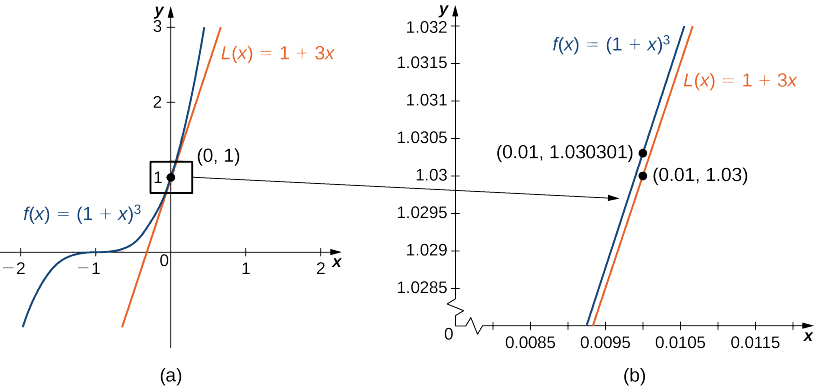
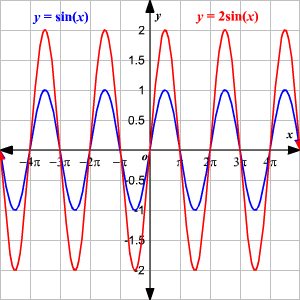
Easy as pi (e) Unlock StepbyStep Natural Language Math Input At this point, the y value is e 2 ≈ 739 Since the derivative of e x is e x, then the slope of the tangent line at x = 2 is also e 2 ≈ 739 We can see that it is true on the graph 1 2 3 4 5 1 2 1 2 3 4 5 6 7 x y (2, 739) slope = 739 y = e x \displaystyle {y}= {e}^ {x} y = exAt this point, students should know what the graph of y = sin(x) looks like Lets explore Parameter a y = a sin(x) Have students predict what they think the graphs of y = 2 sin(x) and y = ½ sin(x) will look like The purple curve is the sine graph The red curve is the transformation y = 2 sin(x) y = ½ sin(x)




Curve Sketching




Find The Area Between The Graph Y E X Sin X X Geq 0 And The X Axis Calculate The Area Of The Area Mathematics Stack Exchange
Properties of Trigonometric Functions The properties of the 6 trigonometric functions sin (x), cos (x), tan (x), cot (x), sec (x) and csc (x) are discussed These include the graph, domain, range, asymptotes (if any), symmetry, x and y intercepts and maximum and minimum points



How Do You Graph Y Sinx 1 Over The Interval 0 X 360 Socratic
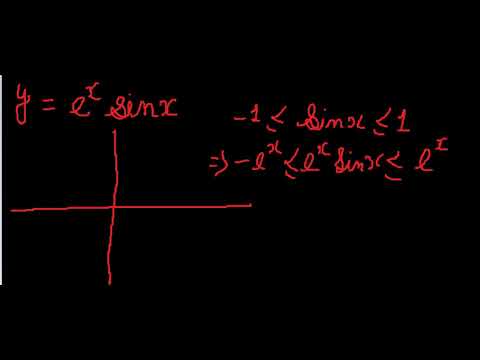



Graph Of Y E Xsinx Youtube
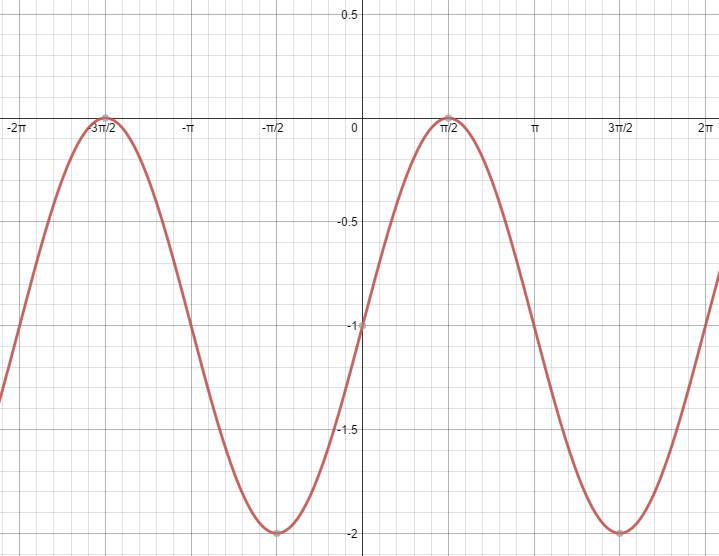



How Do You Graph Y Sin X 1 Socratic
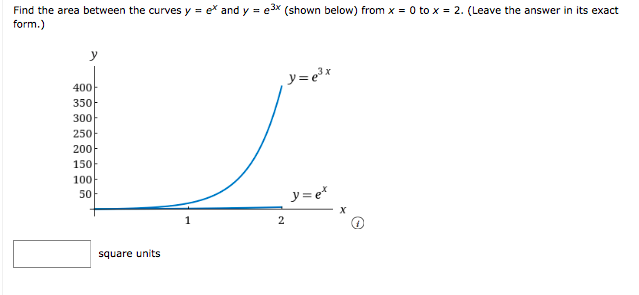



Answered Find The Area Between The Curves Y E Bartleby



Python Plot Sine Wave Function Sin X W Matplotlib



Y E X



1 Graphs Of Y A Sin X And Y A Cos X



3



Y Xsinx



Function Problem E Sin X Physics Forums




Miscellaneous Graphs Y X Sinx Y Xsinx Y E Xsinx Y X 2 1 X Transformation Lecture 12 Youtube



Write Up 1 Sine Functions Y Asin Bx C And Use Of Algebra Expressor



Solution Can We Find The Area Between Y E X And Y E X Sin X Product Rule Integration By Parts Underground Mathematics



What Is The Graph Of Y E Sinx Quora



Find The Area Of The Region By Given Curves Y 3sinx Y E 5x X 0 And X P 2 Mathskey Com



Basic Functions
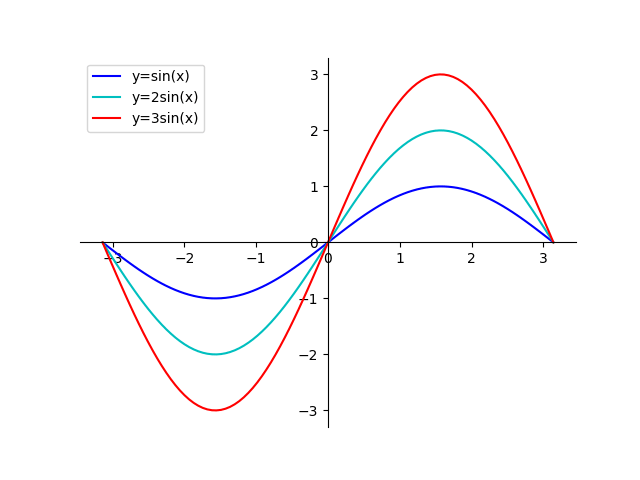



Plot A Function Y F X In Python W Matplotlib
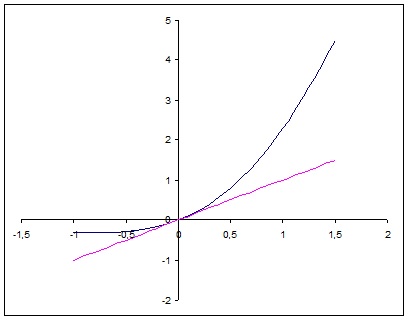



How Do You Find The Equation Of The Tangent Line To The Curve Y E X Sin X At Point 0 0 Socratic
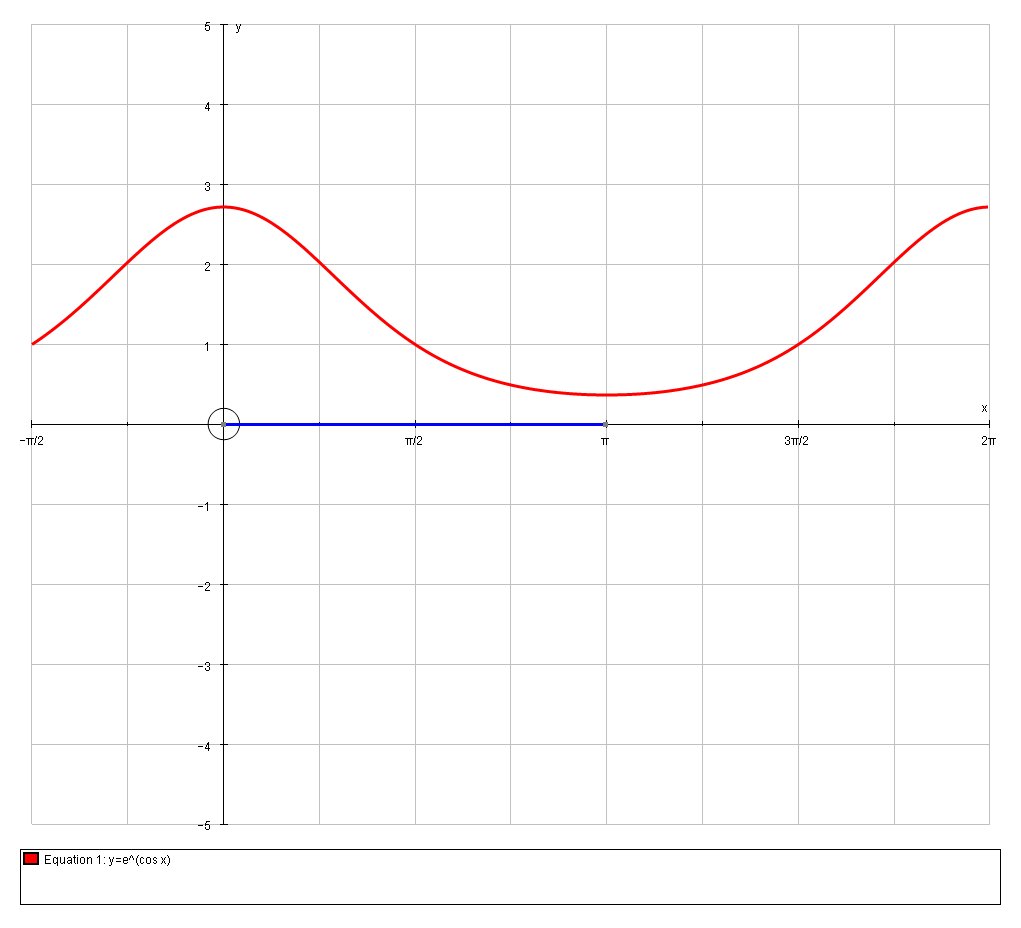



Use Newton S Method To Find The Coordinates Of The Inflection Point Of The Curve Socratic



Tamdistrict Org
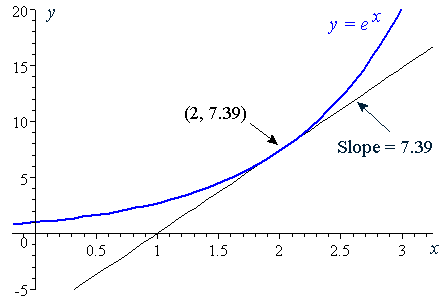



6 Derivative Of The Exponential Function



1



What Is The Y Intercept Of The Tangent To The Curve Y E X Sin X At The Point Where X 0 Enotes Com



Matlab Plotting
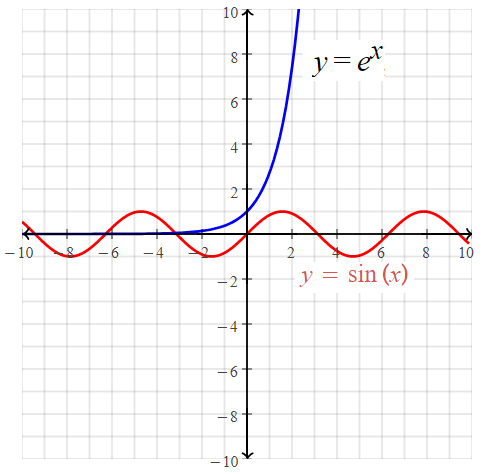



Number Of Solutions Of Y E X And Y Sin X Is



How To Draw A Graph Of Exp X Sinx Quora
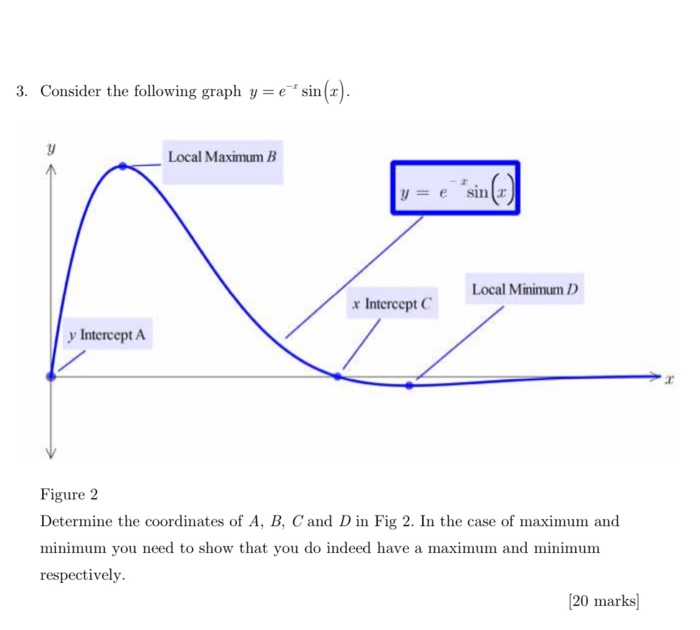



3 Consider The Following Graph Y E Sin X Local Chegg Com



1
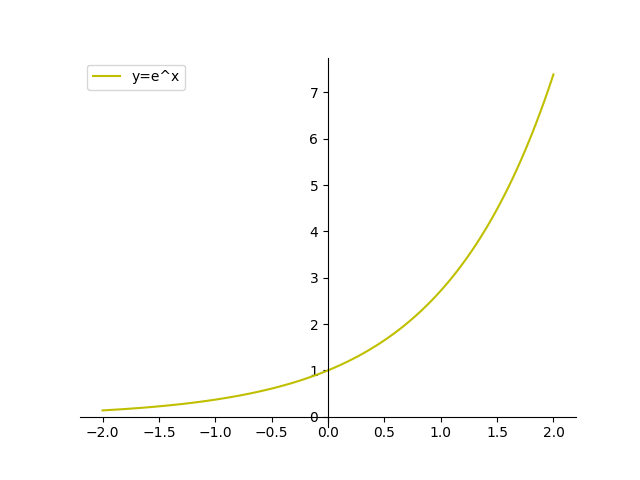



Plot A Function Y F X In Python W Matplotlib




Ppt Download
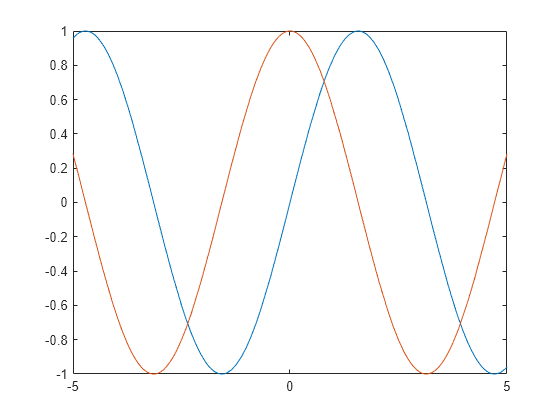



Plot Expression Or Function Matlab Fplot




How Do You Find The Exact Value Of The Area In The First Quadrant Enclosed By Graph Of Y Sinx And Y Cosx Homeworklib
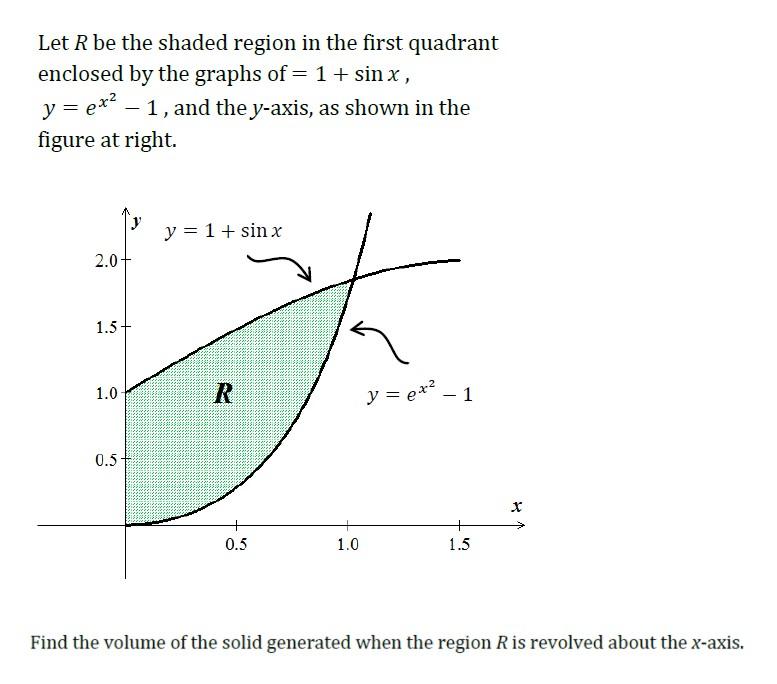



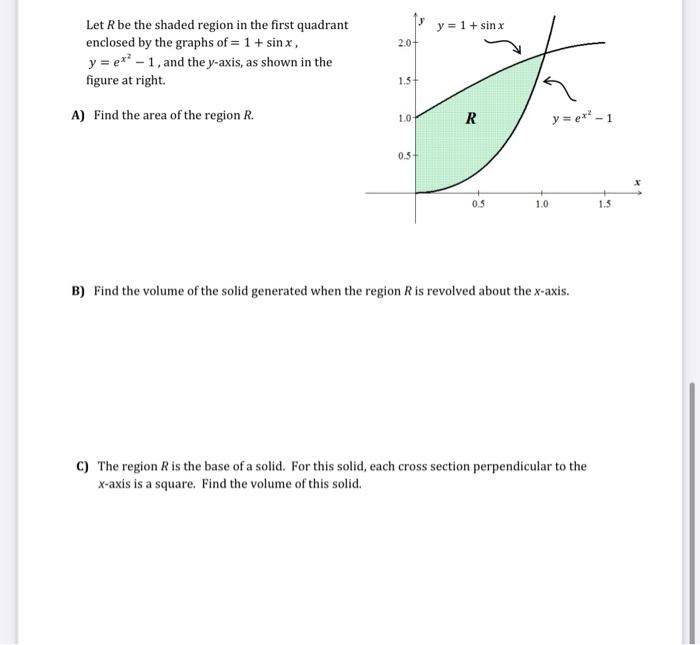
Solved Let R Be The Shaded Region In The First Quadrant Chegg Com




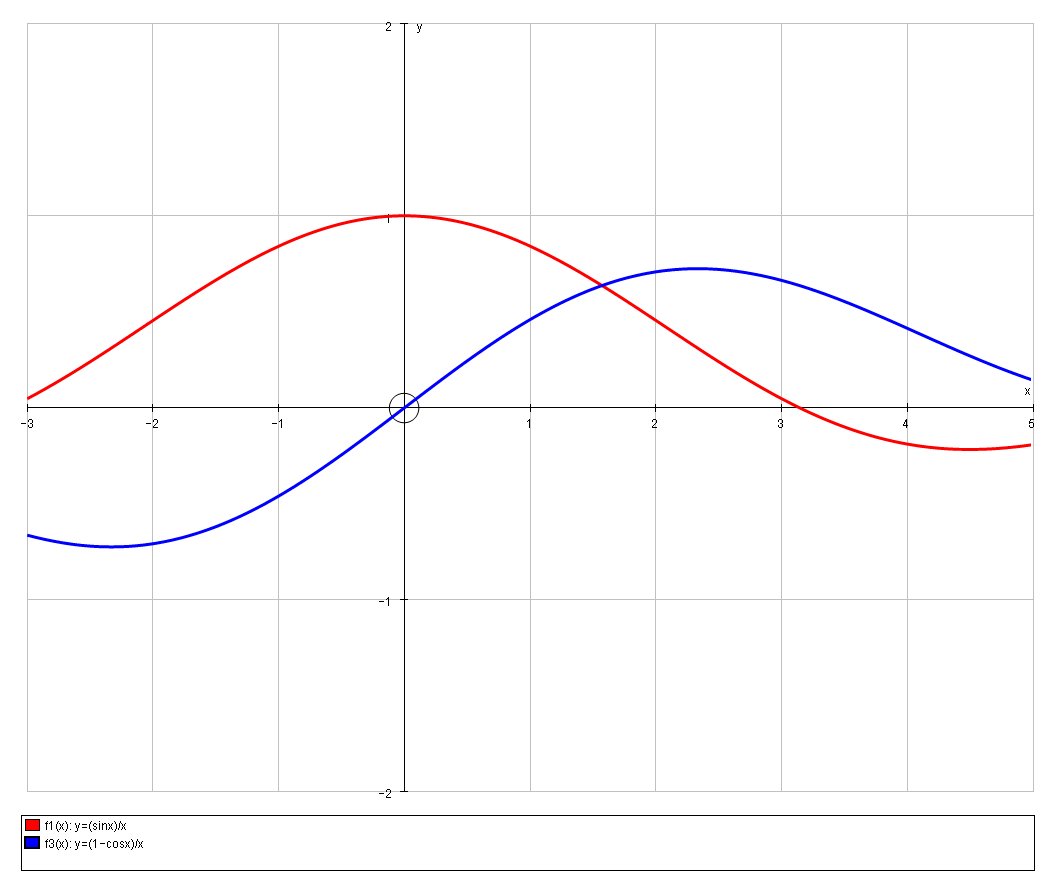
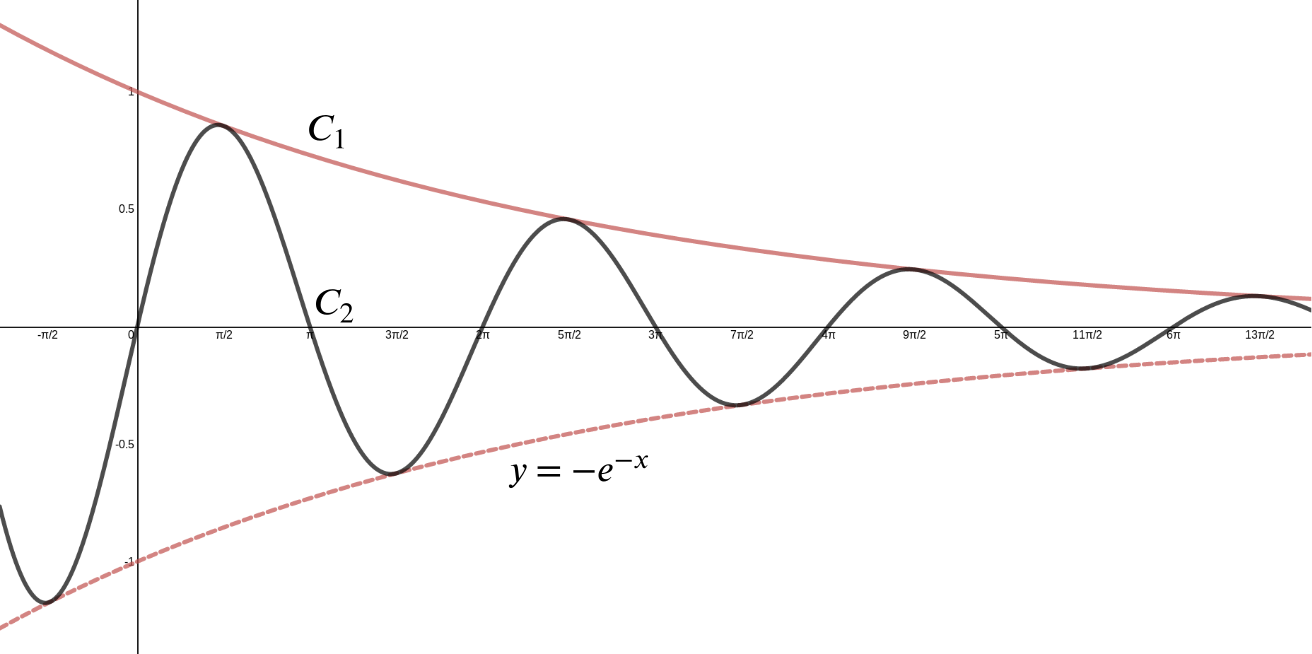
Find The Area Of The Region Between The Curves Y Sin X Y E X 0 And X 7 2 Study Com



Graphsketch




Draw The Graph Of Y Log E Sin X



Y E X Sin X Geogebra




Graphing Sine And Cosine




Y E X Sin X Geogebra



Graphing Sine Function




If Y E X Sinx Then Calculate Dy Dx Youtube



What Is The Graph Of E X Sinx Quora




If Y E X Sin X Cos X Then Show That D 2ydx 2 2 Dydx 2y 0




Find The Critical Value S Of Y E Sin X Cos X 1 Study Com



Write Up 1 Sine Functions Y Asin Bx C And Use Of Algebra Expressor



What Is The Graph For Sinx Y Quora
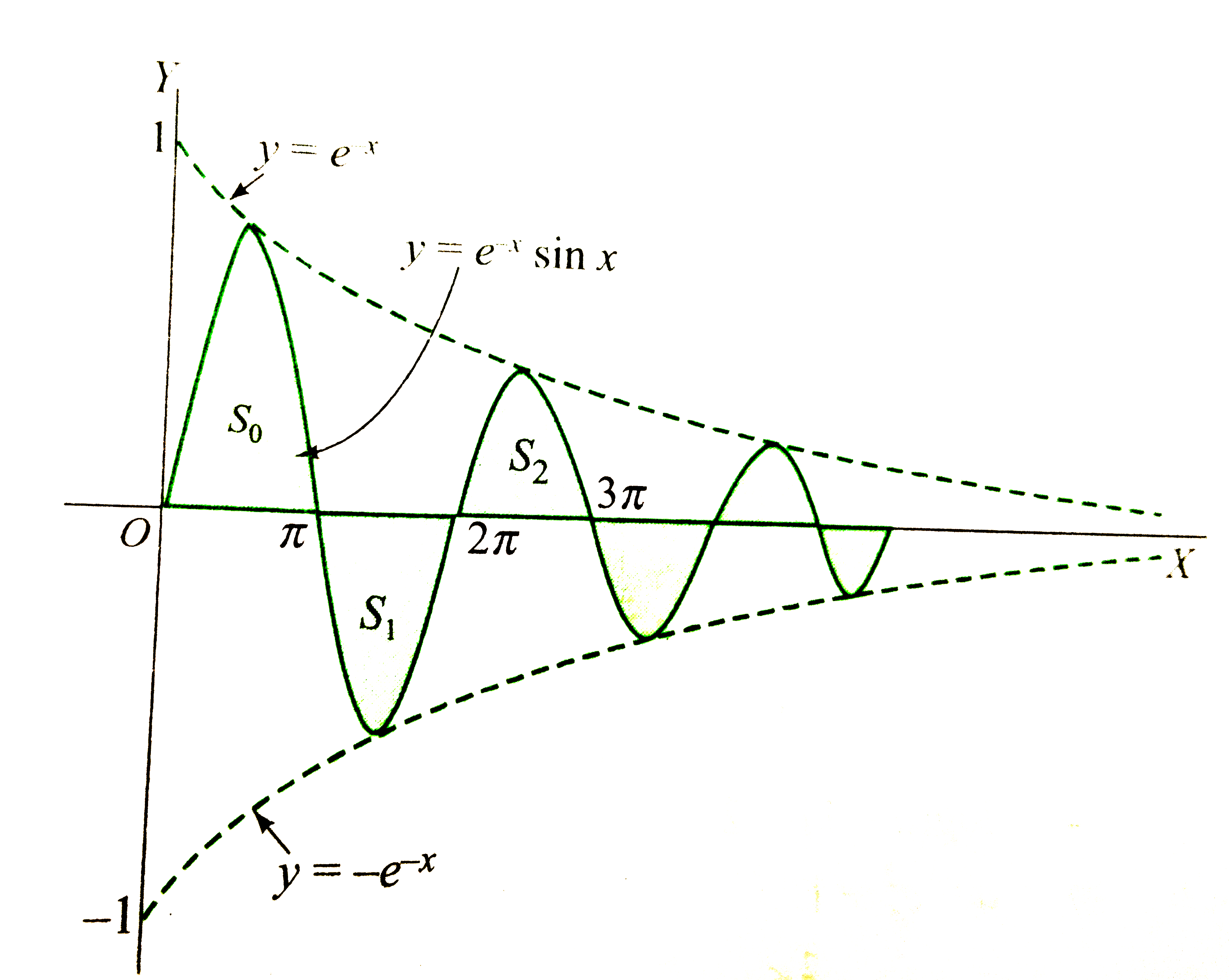



Consider The Area S 0 S 1 S 2 Bounded By The X Axis A
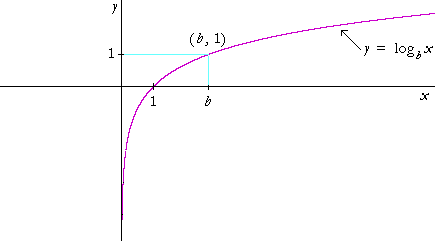



Logarithmic And Exponential Functions Topics In Precalculus




22vb Quick Graph Y Sinx 3 Youtube
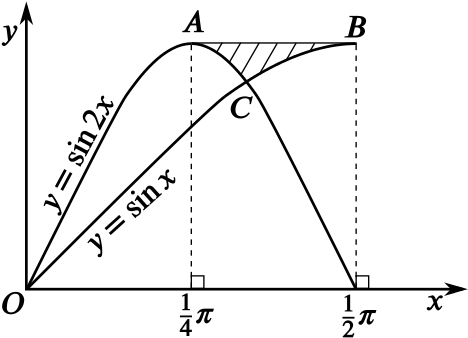



Where Do The Curves Y Sin 2x And Y Sin X Cross Calculus Of Trigonometry Logarithms Underground Mathematics
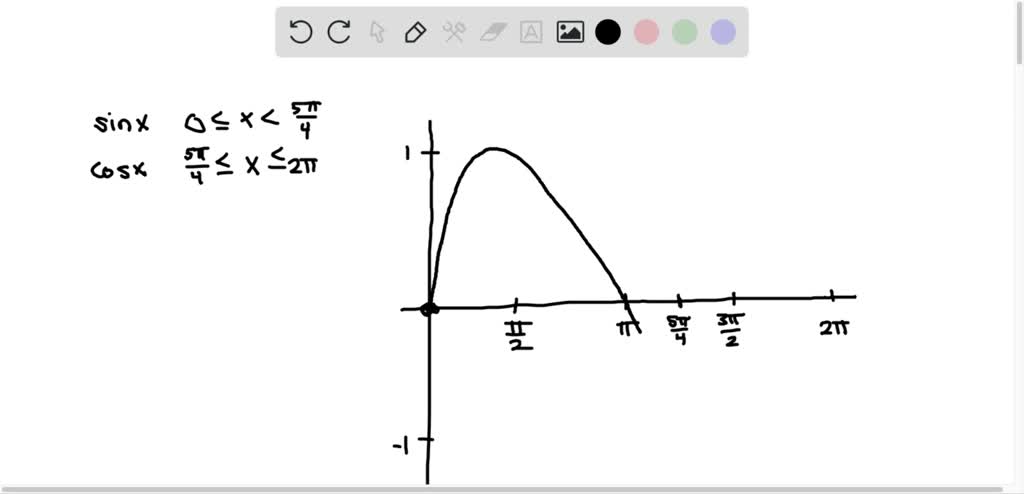



Solved Graph Each Function On A Graphing Calculator Y E 0 3 X Sin Pi X 0 Leq X Leq 10 1 Leq Y Leq 1
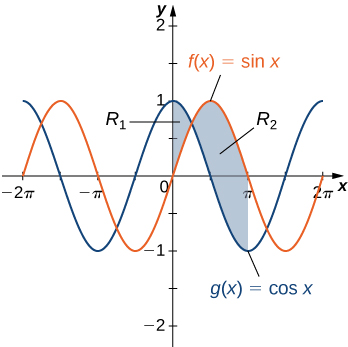



6 1 Areas Between Curves Calculus Volume 1




Solved Each Graph Is A Slight Variation On The Graph Of One Of The Twelve Basic Functions Described In This Section Match The Graph To One Of The Twelve Functions A 1 And Then
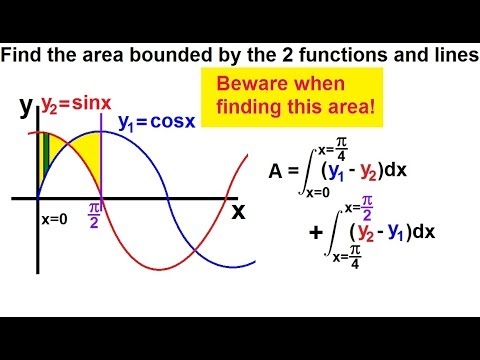



Calculus 2 Integration Finding The Area Between Curves 3 Of 22 Ex 3 Y Sinx Y Cosx Beware Youtube



Math Scene Functions 2 Lesson 6 Inverse Functions
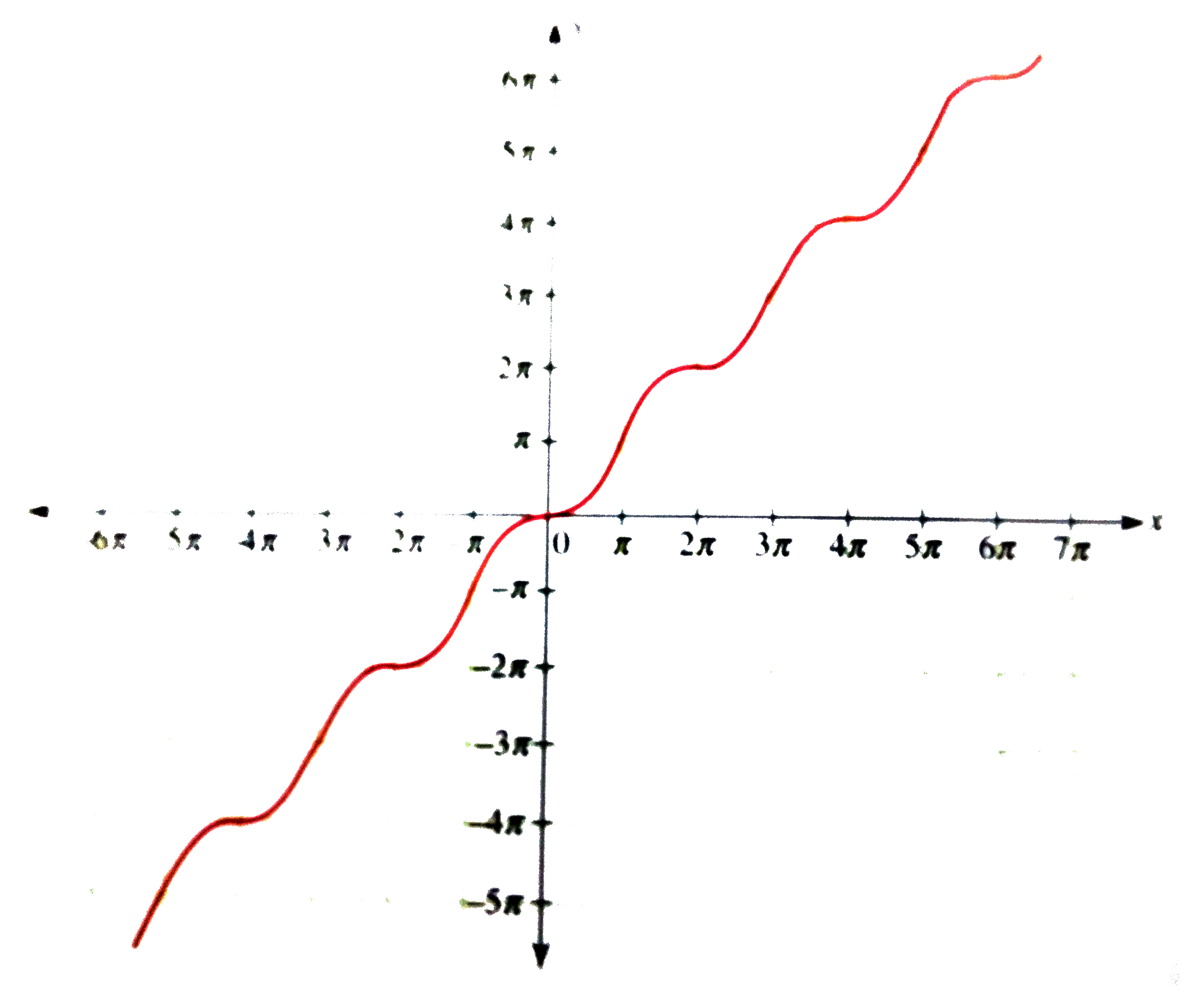



Draw The Graph Of Y X Sinx



1 Graphs Of Y A Sin X And Y A Cos X



Plot Expression Or Function Matlab Fplot



6 1e Exercises Mathematics Libretexts



Solved Y 300 X2 Sin X Y E X3 X2 Let R Be The Chegg Com



Why Can T Y Xe X Be Solved For X Mathematics Stack Exchange



Biomath Trigonometric Functions




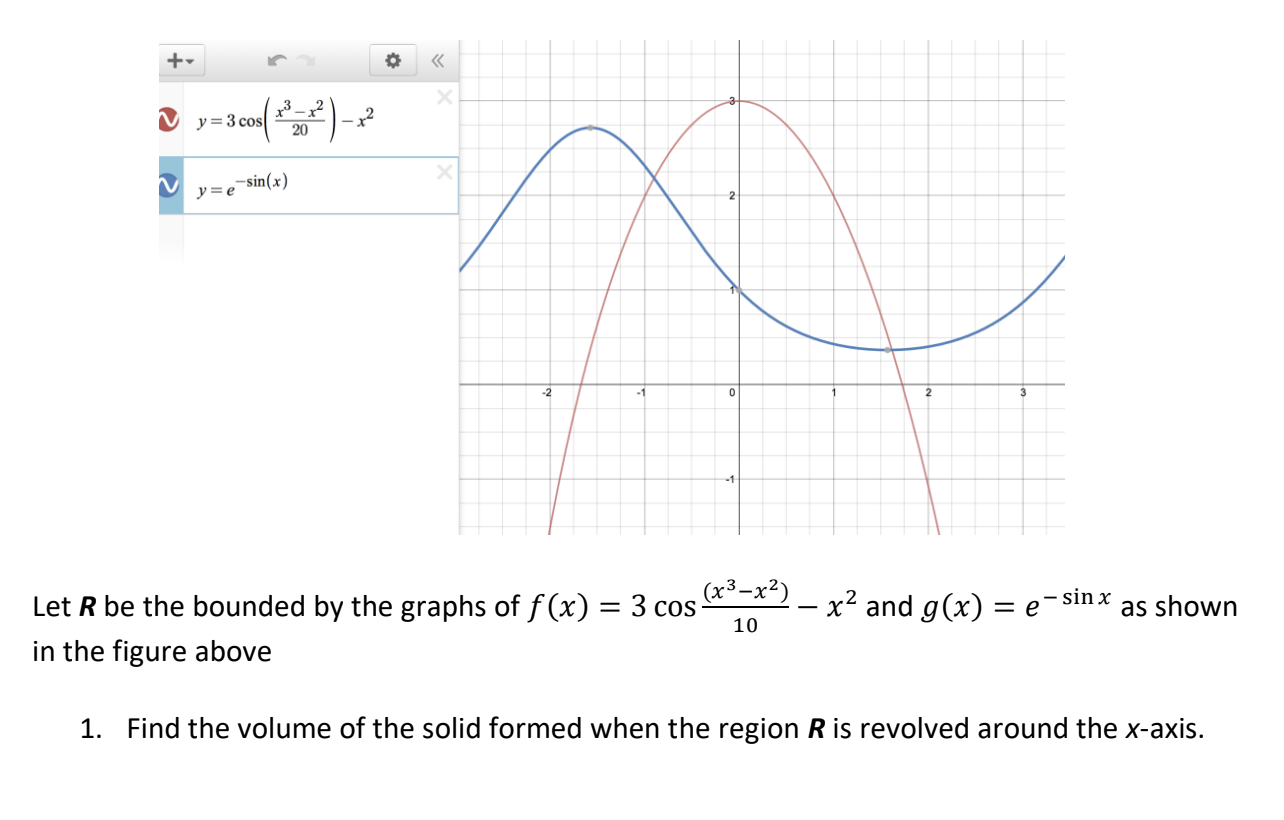
Sketch The Region Enclosed By The Given Curves Decide Whether To Integrate With Respect To X Or Y Draw A Typical Approximating Rectangle And Label Its Height And Width Then Find The Area
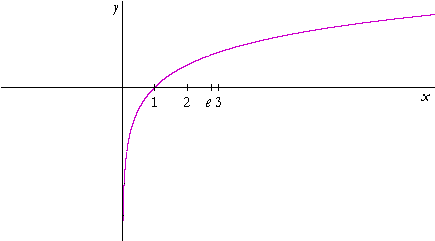



Logarithmic And Exponential Functions Topics In Precalculus




Differentiation With Trig Outcomes Ppt Download



File Indeterminate Form Sin X Over X Far Gif Wikipedia



How Do You Graph Y 3sinx 1 Socratic



Two More Limits The Graph Of The Function F X Sin X X Even Though F 0 Is Undefined The Diagram Shows That F X 1 As X 0 Graphs Of The Functions F X X In Blue G X X Sin 1 X In Green And H X X In Red Notice How The Graphs Of F And H




Solved Suppose F X Sin X And Let F X F E X And G X Chegg Com



How To Find X And Y Intercepts Of Graphs
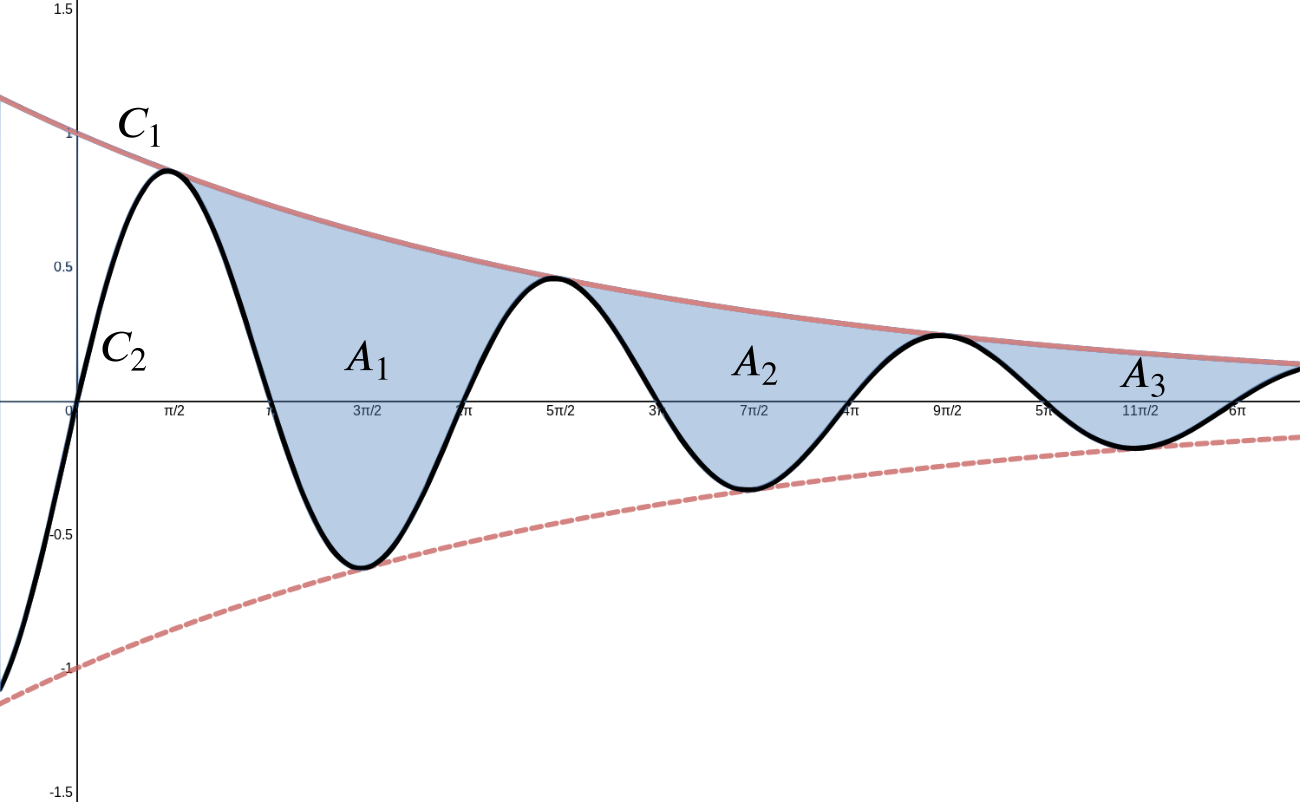



Solution Can We Find The Area Between Y E X And Y E X Sin X Product Rule Integration By Parts Underground Mathematics
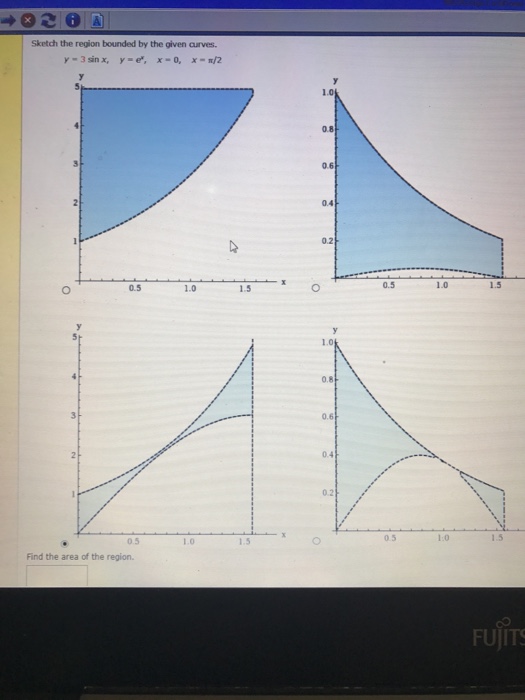



Solved Sketch The Region Bounded By The Given Below Y 3 Chegg Com



Transformation Of The Graph Of Y Sinx Geogebra




Draw The Graph Of Y E X Sin 2pix
).png)



Graph Of Y X Sin X



6 Derivative Of The Exponential Function



0 件のコメント:
コメントを投稿